Qilum is a statistical and utility library supplementing existing statistical libraries, including numpy and scipy. We use numba library to speed up some calculations.

In this first version, we provide several random number generators. They are based on the C++ LOPOR library and the article Canonical local algorithms for spin systems: heat bath and Hasting’s methods. We respect the scipy.stats random number generator interface and any of the scipy.stats classes can be used to initialize qilum classes.

• License MIT
• Contact/Help
• Current version 1.0.0
• Homepage
• Source code
• Distribution/install
• Complete example/tests

• Example: Discrete Walker distribution Dist_walker

# Define a discrete distribution with Walker algorithm
import qilum.stats as qs
walker = qs.Dist_walker(probabilities=[0.2, 0.5, 0.3], values=[0, 10, 2])
# and call the random number generator
rans = walker.rvs(size=100000)

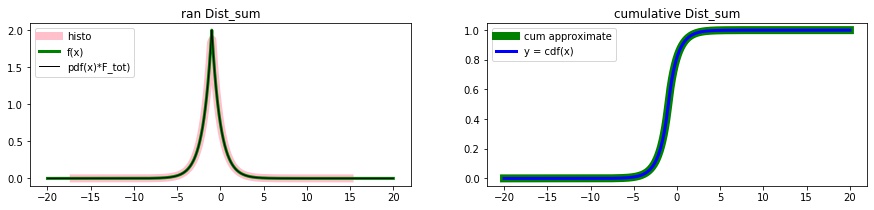
• Example: Sum of distributions Dist_sum

# exponential distributions left and right types
exp_left  = qs.Dist_scale(scipy.stats.expon(),loc_x=-1.000001, scale_x=-1, scale_y=2, name='Exp+')
exp_right = qs.Dist_scale(scipy.stats.expon(),loc_x= -1, scale_x= 1, scale_y=2, name='Exp-')
# sum of the distributions
dist_sum = qs.Dist_sum([exp_left, exp_right]);
# random numbers
rans = dist_sum.rvs(100)

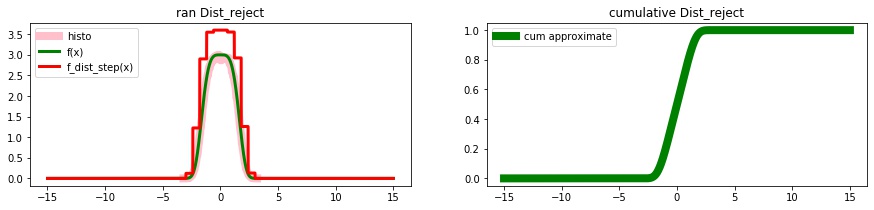
• Example: Rejection method distribution Dist_reject

# generate a random generator for f_f(x)
def f_f(xs): return np.where((xs<-5) | (xs>5), 0, 3.*np.exp(-np.power(xs,4)/10.))
# find a step function above f_f(x)
xs = np.linspace(-6,6, 1001)
ys = f_f(xs)
xs_step, ys_step = qs.f_max(xs, ys, 20)
ys_step *= 1.2 # just to be sure that our step function >= f_f()
# create a distribution for this step function:
hist_dist = scipy.stats.rv_histogram((ys_step, xs_step))
# scale this diribution
cumulative = qs.f_cumulative(xs_step, ys_step)[-1]
dist_step = qs.Dist_scale(hist_dist, scale_y = cumulative, name='dist_step')
# create dist_reject
dist_reject = qs.Dist_reject(dist_step, f_f)
# random numbers
rans = dist_reject.rvs(100)

The main classes are:

• Dist_reject. Construct an exact generator for any probability functions. This is the fastest method when you do not know how to calculate or inverse the cumulative.

• Dist_sum. Construct a sum of known distributions

• Dist_scale. Apply scaling for x and y, for any distributions, even negative scaling for x

• Dist_cubicSpline. Create an approximate random number generator for any functions using cubic spline. If you need an exact random number generator, use Dist_reject. The Dist_cubicSpline can be used instead of scipy.stats.rv_histogram if you need a smooth function

• Dist_walker. Create a very fast random number generator for discrete distributions.

• In addition, we expose the function f_walker() which calculates the parameters of the Walker algorithm

stats Module

Functions

f_cumulative(xs, ys[, normalized])	cumulative calculation
f_max(xs, ys, N)	maximun value ys in N intervals
f_walker(probabilities)	given N probabilities , return a series of N boxes of value mean(probabilities) with 2 indices in each.

Classes

Dist_cubicSpline(x, y[, N_cs])	Distribution for (x,y): cubic splaine approximation for both cumulative ans values
Dist_qilum	Base class for any qilum distribution
Dist_reject(dist_ran, f_fx[, f_tot])	Distribution with rejection method.
Dist_scale(dist[, loc_x, scale_x, scale_y, name])	Distribution scale for x and y: f_new = scale_y*f((x-loc_x)*scale_x)
Dist_sum(dists)	Distribution for a sum of distributions.
Dist_walker(probabilities[, values])	Fast generator for discrete values using the Walker algorithm